Version 1.4.9 features convex envelopes/tesselations, enhanced atom trajectories, complete userguide
With this version we safeguard that the userguide contains at least one example for each and every Action.
The greatest change is however that ... how to put it ... convexification of tesselated envelopes is finally working. This means that volumes of envelopes and thus the space a molecule occupies can be calculated. This is because a convex envelope's volume can be easily calculated via an inner point and general tetrahedrons. If the volume changes can be traced when transforming a non-convex envelope into a convex one, then we also know the volume of the original non-convex envelope. The volume changes however consist of either removing points ("filling up craters") or adding general tetrahedrons, both volume changes are calculable.
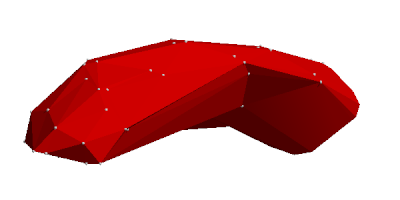
As an example, we give two pictures to illustrate these envelopes, here for the amylose molecule, also known as potato starch.
There is a video among the files attached to this blog post where the progress is shown and the above description of removing points and adding tetrahedrons should become a little bit clearer.
This is a very important change because knowing the volume a molecule takes up is essential in calculating densities and thus knowing how many molecules to fill into a domain. See the upcoming amylose example.
Last but not least trajectories stored in the atom class has been changed. Now, we store them as maps, not as vectors. This means that steps in the trajectory do not necessarily have to be strictly consecutive. For example, when performing a structure optimization (with debugging on) the extra trajectory steps generated for a subset of atoms are no problem anymore.
Attachments (3)
-
nonconvex.png
(10.6 KB
) - added by 10 years ago.
nonconvex envelope of amylose
-
convex.png
(7.9 KB
) - added by 10 years ago.
convex envelope of amylose
-
Convexization_Amylose.mpg
(1.5 MB
) - added by 10 years ago.
movie (done with VMG) showing the progress of the convexification of the initially non-convex envelope
Download all attachments as: .zip

 rss
rss

Comments
No comments.