My last experiments have analysed different conformations of ethane and butane where I've used MolecCuilder to calculate the ground-state energy of various configurations of these two molecules. FOr example, butane I've rotated around its central bond in equidistant steps. This allowed me to compare the resulting potential barriers against the literature.

I'm still on this train of thought: Directly connected to these potential barriers is the question of stability. Given a molecule and a specific configuration, how can I assess the (thermal) stability from ab-initio calculations? And the other question I had in mind: How can I extend this analysis to other (small, organic) molecules?

I will look at the second question first: My inspiration was an article by a former colleague of mine ​[Israels, Maaß, Hamaekers, 2017] on the octet rule in chemical space, Basically, they are generating -- what I call -- saturated molecules using the octet rule (i.e. fully occupied electron orbitals).

It was a low-hanging fruit to add this as some of the necessary ingredients have already been present in MoleCuilder.

1. Saturation of non-hydrogen atoms by placing hydrogens along pre-computed vertices of polyhedra (e.g., for carbon with the four important sp-orbitals, we look at the four corners of a tetrahedra).
2. Encoding knowledge of occupied and unoccupied orbitals per element (e.g., the specific angle in water is mostly because two corners of a tetrahedra are picked)

I then created a larger python script using the pyMoleCuilder library that does the following steps:

1. Start with a "seed" atom in the center of the domain.
2. Saturate the atom.
3. Pick randomly a number of newly added hydrogens (up to a maximum, e.g., 3).
4. Replace this set of picked hydrogens by a single new non-hydrogen atom of a chosen element using the mean position of the hydrogens.
5. Rescale the bond between old and new non-hydrogen atom to typical tabularized bond length (in MoleCuilder called "bond table").
6. Step to the new non-hydrogen.
7. When enough non-hydrogen atoms have been added, stop. Otherwise, go to step 2.
8. Calculate ground-state energy or optimize the created configuration.

In order to then generate "all" molecules of a given set of elements (I've picked {C,N,O}), I don't use random picking but the powerset of all hydrogens up till a given number and execute the procedure for every powerset combination.

One small challenge is the naming. I wanted a representation of the bond graph in the name. Informatics knows all about graphs and there's also a format for specifying them: graph6. There's even tools and websites to generate all (connected) graphs up to certain vertex count: See the ​[House of Graphs] and ​[nauty], on searching and generating graphs. I've added a small action to MoleCuilder that gives the currently selected molecule in graph6 representation and that uses BFS to give the element list starting from the least-connected non-hydrogen atom (ignoring hydrogens).

Let me show you the result for N=1.

graph6	elements	chemical formula	molecule name	energy [Ht]	largest force [Ht]	num neg EV	configuration
Ds_	C	CH4	​Methane	-40.181	5.06882e-10 2.80043e-10 6.06817e-10	18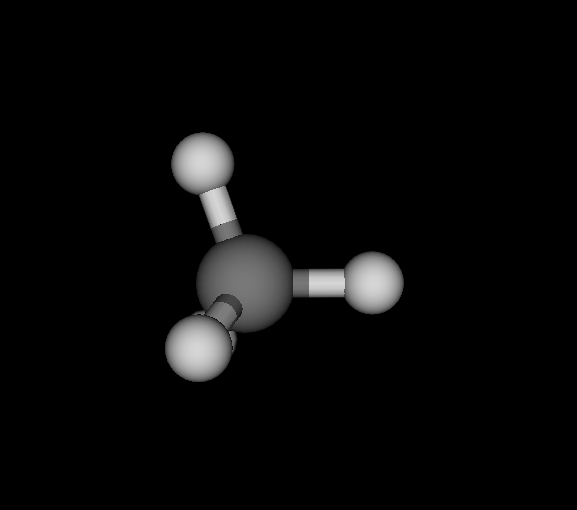
Cs	N	NH3	​Ammonia	-56.166	2.02605e-05 2.88662e-05 4.92678e-05	16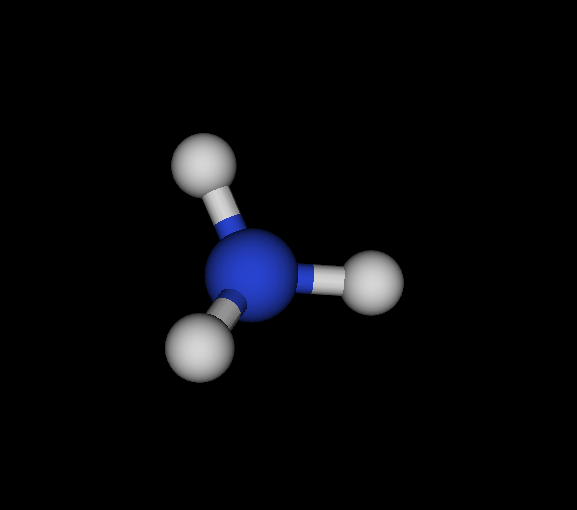
Bo	O	OH2	​Water	-75.985	8.22233e-09 1.18472e-08 2.90999e-11	14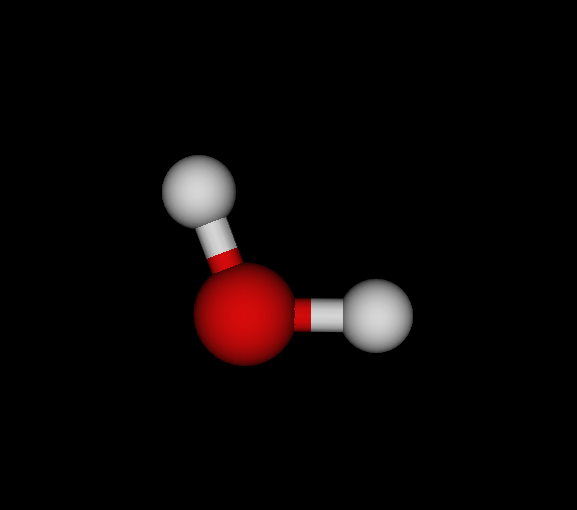

You find the graph6 string (of full graph including hydrogens) first, then the list of elements, the chemical formula and the molecule's name. Moreover, I give the ground state energy (see below for details), the largest remaining force component per dimension and number of negative eigenvectors. Finally, a small graphical representation of the optimized structure (automated snapshot taken with molecuildergui using a small python script). The most important bit about this: It's completely automated. I'm just giving the parameters, run the whole experiment and the output is the above table.

Energy calculations have been done in 6-31G basis (mostly for reasons of computational ease, not accuracy) and either Closed-Shell Hartree-Fock (CLHF) or Moeller-Plesset Perturbation Theory second order (MBPT). As you see, O and C are well-optimized, N is not yet. However, my goal here is not to give accurate ground-state configurations and energies but just show what's possible.

The tables for N from 1 up till 3 are given in the attachments, where you also find the necessary script files.

We added some more complex code for saturating atoms properly. It takes fully into account already present bonds and tries to match to internally stored SphericalPointDistributions as best as possible. This gives really good initial results, i.e. building up molecules just by adding a few carbon, nitrogens and oxygens, when subsequent structure optimization relaxes everything to its proper equilibrium positions.

Moreover, we fixed the fragmentation working on just a subset of atoms, i.e. leaving out saturation water.

In the GUI, the Fragment list can now be properly sorted (and still clicked to get the fragment as set of selected atoms).

FragmentationAutomation will actually fail when the Server is unreachable and not spin forever.

ParseTremoloPotentials is gone, as it is superseded by ParseParticleParameters which is also responsible for parsing partial charges. See also SaveParticleParameters.

Note that for versions in between this and v1.5.0 we refrained from producing debian packages as these did not really bring any good change for the user. Starting from this version, it is again worth to update ... especially with what's coming up!

With v1.4.7 a better hydrogen saturation procedure was implemented.

So far, we dealt with each bond to be saturated one after the other and could handle up to bond degree of three. The problem with the old code was that placement of saturation hydrogen was independent of that for another bond. This could result in hydrogens being placed on top of each other or at least very close. This occurred for example with the SLES molecule when the sulfur bonds were saturated due to its high valency.

Now, we calculate optimal places for saturation globally per molecule prior to the fragmentation procedure. After fragments have been determined and cut bonds need to be saturated, the required positions of the hydrogen are looked up from a table created by this prior calculation. This ensures that hydrogen placed by the saturation of two different bonds are optimally far away from each other.

Note that hydrogen saturation is a perturbation of the underlying Fock matrix (in the case a Hartree-Fock solver is used). Hence, resulting energies are affected and will now be slightly different.

There is a new make target extracheck that runs when mpqc (​http://www.mpqc.org/) is installed and can found in the path: It compares resulting values for some molecules against stored ones. There, relative differences (for bond order of 3) of up to 1e-5 are admissable!

Furthermore, the version now compiles on Ubuntu 14.04 systems. Some changes were necessary due to new boost and gcc versions.

Last but not least a simple Structural Optimization procedure based on the fragmentation has been implemented. This is so far just using calculated forces and some fixed stepwidth dampening scheme to look for the minimum. Enhancements are coming up but will take some more time.