Experiment: Conformational analysis of ethane
In today's blog entry we look at the simple ethane molecule. More precisely, we interested in the rotational change between two of its conformations: staggered and the eclipsed.
We are interested in the energy barrier between these two conformations.
Let's first build the ethane molecule from scratch. We fire up molecuildergui and add two carbon atoms about 1.6 Angström apart from one another using add-atom. Then, we add hydrogens with saturate-atoms after having selected both carbons (either by clicking on them) or using select-all-atoms. The result looks quite reasonable already but the structure is not optimized. This we make up leeway by optimize-structure with 500 steps at a deltat of 2.5, all force components are then below 7e-7 a.u.. Note that beforehand we have used set-parser-parameters of mpqc to have a basis set of 6-31G and theory to MBPT2, moreover used random-perturbation with set-random-number-distribution as uniform_01 to randomly perturb all positions by at most 0.05 Angström. The latter shakes the configuration out of any possible unstable equilibrium. We obtain a final energy of -79.38819 Ht.
Now we step on to the actual analysis of the conformational change. We use a little python script (see C2H6_rotate-bond.py) using the python module pyMolecuilder of MoleCuilder (version 1.6.1). The script rotates via rotate-around-bond one end of the ethane molecule by a prescribed angle, where we use select-atom-by-element to select both carbon atoms and thus specifying the bond around which to rotate. In total we go through the 360 degrees in steps of 5 degrees. After each rotation, the energy of the molecule in vacuum is calculated using MPQC by the action triplet fragment-molecule, fragment-automation, analyse-fragment-results. Before each rotation, we step on to the next discrete time step using step-world-time such that we obtain the complete trajectory of the rotation on output via output-as.
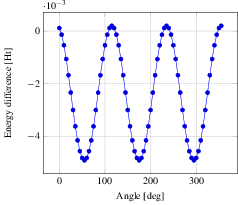
In the figure we see nicely the change in energy between the staggered and the eclipsed conformation, each occurring thrice over the range of 360 degrees. Note that we plot against the lowest energy of -79.38819027 Ht, hence negative difference actually means a higher energy. From the graph we read off the energy difference as roughly 0.005 Ht, equivalent to 0.136 eV. At room temperature of 300 Kelvin, we have a average thermal energy of 0.026 eV. Hence, the eclipsed state's probability is about $\exp(-0.136eV/(k_B * 300 K)) = 0.0052$ with respect to the staggered one, i.e. ethane will remain mostly in the staggered state.
For a nicer and more elaborate discussion of the underlying chemistry, see here. There, it is suggested to look also at butane. And one should replace one hydrogen atom on either end of the ethane molecule by a methyl group.
But we will leave this for the next blog entry ...
Attachments (2)
-
C2H6-rotational_barrier.png
(10.4 KB
) - added by 9 years ago.
staggered-eclipsed energy barrier C2H6
-
C2H6_rotate-bond.py
(2.1 KB
) - added by 9 years ago.
python script using pyMoleCuilder for rotating ethane around its C-C bond
Download all attachments as: .zip

 rss
rss
Comments
No comments.